On Relational Lattice complements, pseudocomplements, distributivity and Boolean algebras
Quote from AntC on June 24, 2021, 10:52 amQuote from Vadim on June 22, 2021, 1:51 pmP.S. I don't follow your comment about distributivity of the lattice of header relations.
I mean that if you take any relation and emptify it, you can form all the projections on to subsets of its heading, down to and including the empty heading subset
DUM. Or rather I mean "up to"DUMin the lattice ordering. That forms a Boolean algebra; it's distributive; but what might be more important: it's uniquely complemented.Let's think about Lattice complements more generally (does this thinking hold?) ...
- Within a Relational Lattice, every element
xhas a complementzs.t.x NatJoin z = R10(R10is lattice bottom aka DUMPTY);x InnerUnion z = R01(R01is lattice top aka DEE).- In terms of 'how to build' the complement: the heading of the complement is all the attributes in the Lattice's 'Universe', minus the heading of
x; the body of the complement is either empty (ifxis non-empty), or must contain at least one tuple (ifxis empty).- Complements are not necessarily unique. Specifically if the body of
xis empty, its complements' bodies might have any number of tuples from one up to all possible tuples for that complemented heading. ("All possible tuples" would be what's generated by Appendix A<NOT> rwhereris an empty relation with that complemented heading.)- The M3 non-distributive lattice does not appear embedded within any Relational Lattice. The N5 lattice does appear embedded -- in fact that's exactly what causes the non-uniqueness of complements: in that diagram,
a's complement could beborc.- If complements are not unique, we can at least say all candidate complements
z1, z2, ...have the same heading -- that isz1 NatJoin DUM = z2 NatJoin DUM = .... So we can use the lattice ordering to define the 'pseudocomplement' as "the greatest element y such that x ∧ y = 0." [wikipedia] IOW s.t.x NatJoin y = DUMPTY.- If any element has non-unique complements, then
DUM's complements must be non-unique -- becauseDUM's complements have maximum possible heading of the whole 'Universe'; whose cardinality is up to the Cartesian Product of the attribute types within the Universe.DUMis the highest (in Lattice ordering) relation with an empty body. IOW the highest with non-unique complements.I really hate to be relying on the Lattice's 'Universe' of attributes, or on maximal/infinite cardinality relations. So this might be a more palatable line of attack -- if it holds:
- Pick some arbitrary non-empty element
xs.t.x InnerUnion DUM = DEE & x NatJoin DUM < DUM. (That's why we need non-empty.)- Form the convex sublattice with
DEEas sublattice top,x NatJoin DUMas bottom.- Every element has a complement within the sublattice -- again not necessarily unique, but the same characteristics of non-unique complements apply as above.
- In particular, if any element has a non-unique complement,
DUMcertainly does (within the sublattice); and all candidate complements have the same heading.- Candidate complements for
DUMin fact have headingx NatJoin DUM.
Quote from Vadim on June 22, 2021, 1:51 pmP.S. I don't follow your comment about distributivity of the lattice of header relations.
I mean that if you take any relation and emptify it, you can form all the projections on to subsets of its heading, down to and including the empty heading subset DUM. Or rather I mean "up to" DUM in the lattice ordering. That forms a Boolean algebra; it's distributive; but what might be more important: it's uniquely complemented.
Let's think about Lattice complements more generally (does this thinking hold?) ...
- Within a Relational Lattice, every element
xhas a complementzs.t.x NatJoin z = R10(R10is lattice bottom aka DUMPTY);x InnerUnion z = R01(R01is lattice top aka DEE). - In terms of 'how to build' the complement: the heading of the complement is all the attributes in the Lattice's 'Universe', minus the heading of
x; the body of the complement is either empty (ifxis non-empty), or must contain at least one tuple (ifxis empty). - Complements are not necessarily unique. Specifically if the body of
xis empty, its complements' bodies might have any number of tuples from one up to all possible tuples for that complemented heading. ("All possible tuples" would be what's generated by Appendix A<NOT> rwhereris an empty relation with that complemented heading.) - The M3 non-distributive lattice does not appear embedded within any Relational Lattice. The N5 lattice does appear embedded -- in fact that's exactly what causes the non-uniqueness of complements: in that diagram,
a's complement could beborc. - If complements are not unique, we can at least say all candidate complements
z1, z2, ...have the same heading -- that isz1 NatJoin DUM = z2 NatJoin DUM = .... So we can use the lattice ordering to define the 'pseudocomplement' as "the greatest element y such that x ∧ y = 0." [wikipedia] IOW s.t.x NatJoin y = DUMPTY. - If any element has non-unique complements, then
DUM's complements must be non-unique -- becauseDUM's complements have maximum possible heading of the whole 'Universe'; whose cardinality is up to the Cartesian Product of the attribute types within the Universe. DUMis the highest (in Lattice ordering) relation with an empty body. IOW the highest with non-unique complements.
I really hate to be relying on the Lattice's 'Universe' of attributes, or on maximal/infinite cardinality relations. So this might be a more palatable line of attack -- if it holds:
- Pick some arbitrary non-empty element
xs.t.x InnerUnion DUM = DEE & x NatJoin DUM < DUM. (That's why we need non-empty.) - Form the convex sublattice with
DEEas sublattice top,x NatJoin DUMas bottom. - Every element has a complement within the sublattice -- again not necessarily unique, but the same characteristics of non-unique complements apply as above.
- In particular, if any element has a non-unique complement,
DUMcertainly does (within the sublattice); and all candidate complements have the same heading. - Candidate complements for
DUMin fact have headingx NatJoin DUM.
Quote from Vadim on June 24, 2021, 6:15 pmA nonunique operation is formally a relation, binary in this case. This would demote complement to the role similar to the partial order. Are there axioms besides the two that you exibited in the definition of the complement operation?
Again, I'm for splitting this operation into the two: deterministic unary tuple set complement, and attribute inversion. The first one is pretty well behaved, and the second one is little more deficient. If we have tuple complement then , we can express TTM Algebra A operation [latex]\lhd OR \rhd[/latex], distributivity of natural join over [latex]\lhd OR \rhd[/latex], etc.
A nonunique operation is formally a relation, binary in this case. This would demote complement to the role similar to the partial order. Are there axioms besides the two that you exibited in the definition of the complement operation?
Again, I'm for splitting this operation into the two: deterministic unary tuple set complement, and attribute inversion. The first one is pretty well behaved, and the second one is little more deficient. If we have tuple complement then , we can express TTM Algebra A operation \lhd OR \rhd, distributivity of natural join over \lhd OR \rhd, etc.
Quote from AntC on June 25, 2021, 2:24 amQuote from Vadim on June 24, 2021, 6:15 pmA nonunique operation is formally a relation, binary in this case. This would demote complement to the role similar to the partial order. Are there axioms besides the two that you exibited in the definition of the complement operation?
Pseudocomplements formally are functions, not relations.
There's much more than two axioms indicated in my first post (I'm not saying all of these are 'useful', whatever that might mean): every element has a complement; for a given element, all candidate complements have the same heading; all elements have a unique pseudocomplement (note that candidate complements are partially-ordered, not all are comparable, part of what makes the pseudocomplement unique is that it is comparable to every candidate); non-empty relations have unique complements;
DUMis the max element amongst those that have non-unique complements.I think this also holds: every convex sublattice of a Relational Lattice is uniquely relatively pseudocomplemented. (The definition of relative (pseudo)complement in the wiki seems to be different to that in the Burris and Sankappanavar text, Def'n 8.6/page 156.) Again if the relative complement is not unique, the 'candidates' have the same heading -- which brings in
DUMeven though it's not an element of the sublattice:
- relative complement =df
ds.t. foralla ≤ b ≤ c. b ^ d = a & b v d = c. relative pseudocomplement is the max suchd.- Note
a ≤ b ≤ cdefines a convex sublattice: we can't just pick any random elements from the full lattice.- Furthermore, if there are non-unique complements, each convex sublattice must contain a 'relative
DUM' that has minimum heading and minimum body for that heading, relative to other elements in the sublatticea ≤ c. In that case 'relativeDUM' is not nec. adjacent to sublattice topc.- OTOH depending on the choice for
a, c, it might be that allb's have unique complements -- then there is no 'relativeDUM'. (In fact we have a Boolean algebra.)Again, I'm for splitting this operation into the two: deterministic unary tuple set complement, and attribute inversion. The first one is pretty well behaved, and the second one is little more deficient.
I'm not trying to introduce extra operations into the algebra. We already have enough to be expressively complete. My Algebra's complement-like operations are
Not Matching, Remove-- that is, relative complements. I'm in this thread exploring properties ofDUM.If we have tuple complement then , we can express TTM Algebra A operation [latex]\lhd OR \rhd[/latex], distributivity of natural join over [latex]\lhd OR \rhd[/latex], etc.
No I don't want domain-dependent operators. Appendix A says that in practice/in Tutorial D,
<OR>will be limited to operands with the same heading. ThenInnerUniongives the same result. (AndNatJoinis distributive overInnerUnionproviding operands same heading. We just need to fixDUMso we can express 'same heading'.)
Quote from Vadim on June 24, 2021, 6:15 pmA nonunique operation is formally a relation, binary in this case. This would demote complement to the role similar to the partial order. Are there axioms besides the two that you exibited in the definition of the complement operation?
Pseudocomplements formally are functions, not relations.
There's much more than two axioms indicated in my first post (I'm not saying all of these are 'useful', whatever that might mean): every element has a complement; for a given element, all candidate complements have the same heading; all elements have a unique pseudocomplement (note that candidate complements are partially-ordered, not all are comparable, part of what makes the pseudocomplement unique is that it is comparable to every candidate); non-empty relations have unique complements; DUM is the max element amongst those that have non-unique complements.
I think this also holds: every convex sublattice of a Relational Lattice is uniquely relatively pseudocomplemented. (The definition of relative (pseudo)complement in the wiki seems to be different to that in the Burris and Sankappanavar text, Def'n 8.6/page 156.) Again if the relative complement is not unique, the 'candidates' have the same heading -- which brings in DUM even though it's not an element of the sublattice:
- relative complement =df
ds.t. foralla ≤ b ≤ c. b ^ d = a & b v d = c. relative pseudocomplement is the max suchd. - Note
a ≤ b ≤ cdefines a convex sublattice: we can't just pick any random elements from the full lattice. - Furthermore, if there are non-unique complements, each convex sublattice must contain a 'relative
DUM' that has minimum heading and minimum body for that heading, relative to other elements in the sublatticea ≤ c. In that case 'relativeDUM' is not nec. adjacent to sublattice topc. - OTOH depending on the choice for
a, c, it might be that allb's have unique complements -- then there is no 'relativeDUM'. (In fact we have a Boolean algebra.)
Again, I'm for splitting this operation into the two: deterministic unary tuple set complement, and attribute inversion. The first one is pretty well behaved, and the second one is little more deficient.
I'm not trying to introduce extra operations into the algebra. We already have enough to be expressively complete. My Algebra's complement-like operations are Not Matching, Remove -- that is, relative complements. I'm in this thread exploring properties of DUM.
If we have tuple complement then , we can express TTM Algebra A operation \lhd OR \rhd, distributivity of natural join over \lhd OR \rhd, etc.
No I don't want domain-dependent operators. Appendix A says that in practice/in Tutorial D, <OR> will be limited to operands with the same heading. Then InnerUnion gives the same result. (And NatJoin is distributive over InnerUnion providing operands same heading. We just need to fix DUM so we can express 'same heading'.)
Quote from Vadim on June 25, 2021, 5:48 pmOperation is formally a function. Pseudo-complement expressed as a binary relation (infix @) would be:
x ^ y = y ^ x. (x ^ y) ^ z = x ^ (y ^ z). x ^ (x v y) = x. x v y = y v x. (x v y) v z = x v (y v z). x v (x ^ y) = x. R10 = R10 ^ x. R01 = R01 v x. x < y <-> x ^ y = x. y @ z <-> (y ^ z = R10 & y v z = R01) .However, I struggle to find additional axioms which would make it [deterministic] operation:
y @ z & y @ x -> x = z.As defined above, the @ relation doesn't honor the weakened Relational Lattice version of Complementation Law (FDI):
y @ z -> (x ^ y) v (x ^ z).Also, I doubt you'll be able to express [latex]R00[/latex] purely algebraically in terms of [latex]\{R_{01},R_{10},\vee,\wedge,\triangleleft COMPL \triangleright\}[/latex], where [latex]\triangleleft COMPL \triangleright[/latex] is deterministic operation. I've run QBQL expression harvesting, which progressed to quite lengthy formulas, and found nothing. However, when we split the [latex]\triangleleft COMPL \triangleright[/latex] into tuple set and attribute set complement operations, then, as I reported before, it is expressible:
R00 = ((x' ^ x)` ^ x)`.Again, in my system [latex]\triangleleft COMPL \triangleright[/latex] is derived operation
[latex]\triangleleft COMPL \triangleright x = (x')` [/latex]
honoring the FDI law as well:
x = (x ^ y) v (x ^ (y')`).
Operation is formally a function. Pseudo-complement expressed as a binary relation (infix @) would be:
x ^ y = y ^ x. (x ^ y) ^ z = x ^ (y ^ z). x ^ (x v y) = x. x v y = y v x. (x v y) v z = x v (y v z). x v (x ^ y) = x. R10 = R10 ^ x. R01 = R01 v x. x < y <-> x ^ y = x. y @ z <-> (y ^ z = R10 & y v z = R01) .
However, I struggle to find additional axioms which would make it [deterministic] operation:
y @ z & y @ x -> x = z.
As defined above, the @ relation doesn't honor the weakened Relational Lattice version of Complementation Law (FDI):
y @ z -> (x ^ y) v (x ^ z).
Also, I doubt you'll be able to express R00 purely algebraically in terms of \{R_{01},R_{10},\vee,\wedge,\triangleleft COMPL \triangleright\}, where \triangleleft COMPL \triangleright is deterministic operation. I've run QBQL expression harvesting, which progressed to quite lengthy formulas, and found nothing. However, when we split the \triangleleft COMPL \triangleright into tuple set and attribute set complement operations, then, as I reported before, it is expressible:
R00 = ((x' ^ x)` ^ x)`.
Again, in my system \triangleleft COMPL \triangleright is derived operation
\triangleleft COMPL \triangleright x = (x')`
honoring the FDI law as well:
x = (x ^ y) v (x ^ (y')`).
Quote from AntC on June 26, 2021, 6:32 amQuote from Vadim on June 25, 2021, 5:48 pmOperation is formally a function. Pseudo-complement expressed as a binary relation (infix @) would be:
x ^ y = y ^ x.(x ^ y) ^ z = x ^ (y ^ z).x ^ (x v y) = x.x v y = y v x.(x v y) v z = x v (y v z).x v (x ^ y) = x.R10 = R10 ^ x.R01 = R01 v x.x < y <-> x ^ y = x.y @ z <-> (y ^ z = R10 & y v z = R01) .x ^ y = y ^ x. (x ^ y) ^ z = x ^ (y ^ z). x ^ (x v y) = x. x v y = y v x. (x v y) v z = x v (y v z). x v (x ^ y) = x. R10 = R10 ^ x. R01 = R01 v x. x < y <-> x ^ y = x. y @ z <-> (y ^ z = R10 & y v z = R01) .x ^ y = y ^ x. (x ^ y) ^ z = x ^ (y ^ z). x ^ (x v y) = x. x v y = y v x. (x v y) v z = x v (y v z). x v (x ^ y) = x. R10 = R10 ^ x. R01 = R01 v x. x < y <-> x ^ y = x. y @ z <-> (y ^ z = R10 & y v z = R01) .However, I struggle to find additional axioms which would make it [deterministic] operation:
y @ z & y @ x -> x = z.But you haven't defined Pseudo-complement. You've defined only 'candidate' complement. You need to say Pseudo-complement is max of the candidates.
I have a function working fine, I've added the pseudocomplement axioms from the wiki:
x ^ absPCompl(x) = R10. x v absPCompl(x) = R01. x ^ z = R10 & x v z = R01 -> absPCompl(x) ^ z = z. % PCompl is max of candidate complements absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)).I'm advised that making it a function means the
absPCompl( )automatically exists for all elements.Addit 2: That last is not true in general for relations. And I can't find an alternative reference to double-check if the wiki has got it wrong. That last will fail if:
x, yhave some attributes in common, but no values in common when projected on the common attribs. Then(x ^ y)is empty and double-complement gives an empty/identity, but the double-complements on rhs are all possible tuples for their headings, so the^will yield a non-empty. Removing that last axiom then means it all turns to custard, so ignore next para.[Left in for the historical record, but ignore:] I've also put in some of the axioms I indicated in my first post. Mace4 gives me as a minimum a 5-element model looking just like the N5 non-distrib lattice, and with
R00on the 2-leg side corresponding toahere. Addit oh, ok this is sufficient to give N5:R11 = absPCompl(R00). R11 ^ R1half = R1half. R11 != R1half. absPCompl(R1half) = R00.Since if any element's (ordinary) complement is non-unique, then
R00's is; and all ofR00's complements are betweenR11andR10; I've insertedR1halfas strictly between those two. This forces an asymmetry.BTW this I thought would help, but doesn't make any difference
x v R00 = R01 <-> R00 ^ absPCompl(x) = absPCompl(x).Equiv to Fundamental Empty Relations axiom, but avoiding!=.
As defined above, the @ relation doesn't honor the weakened Relational Lattice version of Complementation Law (FDI):
y @ z -> (x ^ y) v (x ^ z).Of course it doesn't. Those are laws for Boolean algebras. Relational lattices are not Boolean algebras -- exactly because there's embedded N5 sub-lattices.
Also, I doubt you'll be able to express [latex]R00[/latex] purely algebraically ...
Well something among my axioms is generating the N5. I'm exploring more.
I've run QBQL expression harvesting,
Sorry, I won't give credence to QBQL/I've no idea what's inside it. For all I know, it's hard-coded to look for what you want it to find.
I see on that Pseudocomplement wiki there's a 'skeleton' of a Lattice. For Relational lattices that contains: all the empty relations, with
R00as the max of them; and all the relations with all possible tuples for each heading, withR11as the min of them.R11is the pseudocomplement ofR00.
Quote from Vadim on June 25, 2021, 5:48 pmOperation is formally a function. Pseudo-complement expressed as a binary relation (infix @) would be:
x ^ y = y ^ x.(x ^ y) ^ z = x ^ (y ^ z).x ^ (x v y) = x.x v y = y v x.(x v y) v z = x v (y v z).x v (x ^ y) = x.R10 = R10 ^ x.R01 = R01 v x.x < y <-> x ^ y = x.y @ z <-> (y ^ z = R10 & y v z = R01) .x ^ y = y ^ x. (x ^ y) ^ z = x ^ (y ^ z). x ^ (x v y) = x. x v y = y v x. (x v y) v z = x v (y v z). x v (x ^ y) = x. R10 = R10 ^ x. R01 = R01 v x. x < y <-> x ^ y = x. y @ z <-> (y ^ z = R10 & y v z = R01) .x ^ y = y ^ x. (x ^ y) ^ z = x ^ (y ^ z). x ^ (x v y) = x. x v y = y v x. (x v y) v z = x v (y v z). x v (x ^ y) = x. R10 = R10 ^ x. R01 = R01 v x. x < y <-> x ^ y = x. y @ z <-> (y ^ z = R10 & y v z = R01) .However, I struggle to find additional axioms which would make it [deterministic] operation:
y @ z & y @ x -> x = z.
But you haven't defined Pseudo-complement. You've defined only 'candidate' complement. You need to say Pseudo-complement is max of the candidates.
I have a function working fine, I've added the pseudocomplement axioms from the wiki:
x ^ absPCompl(x) = R10. x v absPCompl(x) = R01. x ^ z = R10 & x v z = R01 -> absPCompl(x) ^ z = z. % PCompl is max of candidate complements absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)).
I'm advised that making it a function means the absPCompl( ) automatically exists for all elements.
Addit 2: That last is not true in general for relations. And I can't find an alternative reference to double-check if the wiki has got it wrong. That last will fail if: x, y have some attributes in common, but no values in common when projected on the common attribs. Then (x ^ y) is empty and double-complement gives an empty/identity, but the double-complements on rhs are all possible tuples for their headings, so the ^ will yield a non-empty. Removing that last axiom then means it all turns to custard, so ignore next para.
[Left in for the historical record, but ignore:] I've also put in some of the axioms I indicated in my first post. Mace4 gives me as a minimum a 5-element model looking just like the N5 non-distrib lattice, and with R00 on the 2-leg side corresponding to a here. Addit oh, ok this is sufficient to give N5:
R11 = absPCompl(R00). R11 ^ R1half = R1half. R11 != R1half. absPCompl(R1half) = R00.
Since if any element's (ordinary) complement is non-unique, then R00's is; and all of R00's complements are between R11 and R10; I've inserted R1half as strictly between those two. This forces an asymmetry.
BTW this I thought would help, but doesn't make any difference x v R00 = R01 <-> R00 ^ absPCompl(x) = absPCompl(x). Equiv to Fundamental Empty Relations axiom, but avoiding !=.
As defined above, the @ relation doesn't honor the weakened Relational Lattice version of Complementation Law (FDI):
y @ z -> (x ^ y) v (x ^ z).
Of course it doesn't. Those are laws for Boolean algebras. Relational lattices are not Boolean algebras -- exactly because there's embedded N5 sub-lattices.
Also, I doubt you'll be able to express R00 purely algebraically ...
Well something among my axioms is generating the N5. I'm exploring more.
I've run QBQL expression harvesting,
Sorry, I won't give credence to QBQL/I've no idea what's inside it. For all I know, it's hard-coded to look for what you want it to find.
I see on that Pseudocomplement wiki there's a 'skeleton' of a Lattice. For Relational lattices that contains: all the empty relations, with R00 as the max of them; and all the relations with all possible tuples for each heading, with R11 as the min of them. R11 is the pseudocomplement of R00.
Quote from Vadim on June 26, 2021, 4:13 pmOne way to exclude the inconvenient 5 element model N5 is to introduce tuple complement (AKA Algebra A <NOT>). Without tuple complement the 5 elements of N5 can be interpreted as the following set of relations: [latex]\{ R_{00}, R_{10} = ( \{p\} , \emptyset ), S = ( \{p\} , \{ \langle a \rangle \}), R_{11} = ( \{p\} , \{ \langle a \rangle, \langle b \rangle \}), R_{01} \}[/latex]. There, you can't argue that the 6th relation [latex] ( \{p\} , \{ \langle b \rangle \}) [/latex] should also be there, because you have no way to generate it algebraically from the other 5.
However, with very reasonable axioms for tuple complement it just becomes Boolean Algebra:
% -------- Comments from original proof -------- % Proof 1 at 27.09 (+ 0.28) seconds. % Length of proof is 240. % Level of proof is 41. % Maximum clause weight is 27. % Given clauses 1238. 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal]. 3 x ^ y = y ^ x. [assumption]. 4 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 5 x ^ (x v y) = x. [assumption]. 6 x v y = y v x. [assumption]. 7 (x v y) v z = x v (y v z). [assumption]. 8 x v (x ^ y) = x. [assumption]. 9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption]. 10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)]. 11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption]. 12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)]. 13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption]. 14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])]. 15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)]. 17 x' ^ x = x ^ R00. [assumption]. 18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])]. 19 x'' = x. [assumption]. 20 x ^ absPCompl(x) = R10. [assumption]. 21 x v absPCompl(x) = R01. [assumption]. 22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)]. 23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption]. 24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption]. 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. ...
It appears that your assertions for pseudo-complement are too strong.
For instance, are you sure you need both
x ^ absPCompl(x) = R10.
x v absPCompl(x) = R01.? Wikipedia page that you have referred to has only one of them.
Edit: yes, both
x ^ absPCompl(x) = R10.
<absPCompl>(x v y) = <absPCompl>(x) ^ <absPCompl>(y).
are invalid.
One way to exclude the inconvenient 5 element model N5 is to introduce tuple complement (AKA Algebra A <NOT>). Without tuple complement the 5 elements of N5 can be interpreted as the following set of relations: \{ R_{00}, R_{10} = ( \{p\} , \emptyset ), S = ( \{p\} , \{ \langle a \rangle \}), R_{11} = ( \{p\} , \{ \langle a \rangle, \langle b \rangle \}), R_{01} \}. There, you can't argue that the 6th relation ( \{p\} , \{ \langle b \rangle \}) should also be there, because you have no way to generate it algebraically from the other 5.
However, with very reasonable axioms for tuple complement it just becomes Boolean Algebra:
% -------- Comments from original proof -------- % Proof 1 at 27.09 (+ 0.28) seconds. % Length of proof is 240. % Level of proof is 41. % Maximum clause weight is 27. % Given clauses 1238. 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal]. 3 x ^ y = y ^ x. [assumption]. 4 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 5 x ^ (x v y) = x. [assumption]. 6 x v y = y v x. [assumption]. 7 (x v y) v z = x v (y v z). [assumption]. 8 x v (x ^ y) = x. [assumption]. 9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption]. 10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)]. 11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption]. 12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)]. 13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption]. 14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])]. 15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)]. 17 x' ^ x = x ^ R00. [assumption]. 18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])]. 19 x'' = x. [assumption]. 20 x ^ absPCompl(x) = R10. [assumption]. 21 x v absPCompl(x) = R01. [assumption]. 22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)]. 23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption]. 24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption]. 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. ...
It appears that your assertions for pseudo-complement are too strong.
For instance, are you sure you need both
x ^ absPCompl(x) = R10.
x v absPCompl(x) = R01.
? Wikipedia page that you have referred to has only one of them.
Edit: yes, both
x ^ absPCompl(x) = R10.
<absPCompl>(x v y) = <absPCompl>(x) ^ <absPCompl>(y).
are invalid.
Quote from AntC on June 27, 2021, 11:21 amQuote from Vadim on June 26, 2021, 4:13 pmOne way to exclude the inconvenient 5 element model N5
Errm? I don't want to exclude N5, I want to encourage it. Indeed I want to make sure there's at least one N5 in every model -- that's the reason for the clunky
H1half. It's not "inconvenient"; it's the 'unique characteristic' of Relational lattices.is to introduce tuple complement (AKA Algebra A <NOT>).
That would be one way, but a better way would be to stipulate the full structure, which requires a Boolean algebra for each heading, and therefore requires relative complement.
Without tuple complement the 5 elements of N5 can be interpreted as the following set of relations: [latex]\{ R_{00}, R_{10} = ( \{p\} , \emptyset ), S = ( \{p\} , \{ \langle a \rangle \}), R_{11} = ( \{p\} , \{ \langle a \rangle, \langle b \rangle \}), R_{01} \}[/latex]. There, you can't argue that the 6th relation [latex] ( \{p\} , \{ \langle b \rangle \}) [/latex] should also be there, because you have no way to generate it algebraically from the other 5.
Yes you can: you require that all convex sublattices between
[ x ^ R00, x ]for allxare Boolean algebras -- which they should be. That is, within that interval they're both distributive and uniquely complemented. That is, the algebra is required to have a complement for({p},{⟨a⟩})within[ ({p},{}), ({p},{⟨a⟩,⟨b⟩}) ]. BTW if we include element({p},{⟨b⟩}), we still have a N5 embedded -- in fact there's two. Good!However, with very reasonable axioms for tuple complement it just becomes Boolean Algebra:
I'm not sure this one is reasonable:
1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption].I know I included it in my post; it's like that on one of the references, and that reference has an equivalence not merely implication, but not like that on the others.This one is totally unreasonable/unacceptable:
2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].That's a lattice-wide distribution law. It with the complement law makes the whole lattice a Boolean algebra. Not a Relational lattice.This one I rejected in an Edit to my message:
25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption].It's false in a Relational Lattice, under some scenarios. Furthermore I think it introduces a contradiction against some of the Relational-specific axioms (I see you include the Litak axioms), so I think you end up with a system in which you can prove anything -- that seems what I was getting.% -------- Comments from original proof --------% Proof 1 at 27.09 (+ 0.28) seconds.% Length of proof is 240.% Level of proof is 41.% Maximum clause weight is 27.% Given clauses 1238.1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption].2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].3 x ^ y = y ^ x. [assumption].4 (x ^ y) ^ z = x ^ (y ^ z). [assumption].5 x ^ (x v y) = x. [assumption].6 x v y = y v x. [assumption].7 (x v y) v z = x v (y v z). [assumption].8 x v (x ^ y) = x. [assumption].9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption].10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)].11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption].12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)].13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption].14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])].15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption].16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)].17 x' ^ x = x ^ R00. [assumption].18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])].19 x'' = x. [assumption].20 x ^ absPCompl(x) = R10. [assumption].21 x v absPCompl(x) = R01. [assumption].22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)].23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption].24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption].25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]....% -------- Comments from original proof -------- % Proof 1 at 27.09 (+ 0.28) seconds. % Length of proof is 240. % Level of proof is 41. % Maximum clause weight is 27. % Given clauses 1238. 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal]. 3 x ^ y = y ^ x. [assumption]. 4 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 5 x ^ (x v y) = x. [assumption]. 6 x v y = y v x. [assumption]. 7 (x v y) v z = x v (y v z). [assumption]. 8 x v (x ^ y) = x. [assumption]. 9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption]. 10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)]. 11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption]. 12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)]. 13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption]. 14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])]. 15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)]. 17 x' ^ x = x ^ R00. [assumption]. 18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])]. 19 x'' = x. [assumption]. 20 x ^ absPCompl(x) = R10. [assumption]. 21 x v absPCompl(x) = R01. [assumption]. 22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)]. 23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption]. 24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption]. 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. ...% -------- Comments from original proof -------- % Proof 1 at 27.09 (+ 0.28) seconds. % Length of proof is 240. % Level of proof is 41. % Maximum clause weight is 27. % Given clauses 1238. 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal]. 3 x ^ y = y ^ x. [assumption]. 4 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 5 x ^ (x v y) = x. [assumption]. 6 x v y = y v x. [assumption]. 7 (x v y) v z = x v (y v z). [assumption]. 8 x v (x ^ y) = x. [assumption]. 9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption]. 10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)]. 11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption]. 12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)]. 13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption]. 14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])]. 15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)]. 17 x' ^ x = x ^ R00. [assumption]. 18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])]. 19 x'' = x. [assumption]. 20 x ^ absPCompl(x) = R10. [assumption]. 21 x v absPCompl(x) = R01. [assumption]. 22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)]. 23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption]. 24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption]. 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. ...
It appears that your assertions for pseudo-complement are too strong.
For instance, are you sure you need both
x ^ absPCompl(x) = R10.
x v absPCompl(x) = R01.It does no harm to have both. (One of the wiki pages seems to be saying one follows from the other, but that's including other axioms which perhaps carry more restriction.)
Edit: yes I'm sure I need both. If you have this one only:
x v absPCompl(x) = R01., that's satisfied byx,absPCompl(x)being any two relations with disjoint headings (perhaps a single attribute each) both non-empty. You need the other axiom to make sure theabsPCompl( )is opposite emptiness, and that it has all the attributes not inx, so their^has the heading ofR10.? Wikipedia page that you have referred to has only one of them.
The page on pseudocomplement has only this :
x ∧ x* = 0., which is the one you want to reject, but it does give extra requirements. It does go on to say the definitions necessarily give a1element. There's (at least) three wiki pages: on lattices, on complemented lattices, and on pseudo-complements/p-algebras. Also a page on po-sets. They're not well co-ordinated.Edit: yes, both
x ^ absPCompl(x) = R10.
xbeing empty makesx*non-empty, and vice versa. So one of the operands to the^is empty. So the result is empty. So this holds for Relational lattices.<absPCompl>(x v y) = <absPCompl>(x) ^ <absPCompl>(y).
are invalid.
I editted my message to say the third they give is wrong (your 25 above). Your second one there (24 above) I think does hold. I've gone through the scenarios of same-headings, disjoint-headings, partial overlaps; for both, neither, one empty. Do you have a counter-example?
Quote from Vadim on June 26, 2021, 4:13 pmOne way to exclude the inconvenient 5 element model N5
Errm? I don't want to exclude N5, I want to encourage it. Indeed I want to make sure there's at least one N5 in every model -- that's the reason for the clunky H1half. It's not "inconvenient"; it's the 'unique characteristic' of Relational lattices.
is to introduce tuple complement (AKA Algebra A <NOT>).
That would be one way, but a better way would be to stipulate the full structure, which requires a Boolean algebra for each heading, and therefore requires relative complement.
Without tuple complement the 5 elements of N5 can be interpreted as the following set of relations: \{ R_{00}, R_{10} = ( \{p\} , \emptyset ), S = ( \{p\} , \{ \langle a \rangle \}), R_{11} = ( \{p\} , \{ \langle a \rangle, \langle b \rangle \}), R_{01} \}. There, you can't argue that the 6th relation ( \{p\} , \{ \langle b \rangle \}) should also be there, because you have no way to generate it algebraically from the other 5.
Yes you can: you require that all convex sublattices between [ x ^ R00, x ] for all x are Boolean algebras -- which they should be. That is, within that interval they're both distributive and uniquely complemented. That is, the algebra is required to have a complement for ({p},{⟨a⟩}) within [ ({p},{}), ({p},{⟨a⟩,⟨b⟩}) ]. BTW if we include element ({p},{⟨b⟩}), we still have a N5 embedded -- in fact there's two. Good!
However, with very reasonable axioms for tuple complement it just becomes Boolean Algebra:
I'm not sure this one is reasonable: 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. I know I included it in my post; it's like that on one of the references, and that reference has an equivalence not merely implication, but not like that on the others.
This one is totally unreasonable/unacceptable: 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].That's a lattice-wide distribution law. It with the complement law makes the whole lattice a Boolean algebra. Not a Relational lattice.
This one I rejected in an Edit to my message: 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. It's false in a Relational Lattice, under some scenarios. Furthermore I think it introduces a contradiction against some of the Relational-specific axioms (I see you include the Litak axioms), so I think you end up with a system in which you can prove anything -- that seems what I was getting.
% -------- Comments from original proof --------% Proof 1 at 27.09 (+ 0.28) seconds.% Length of proof is 240.% Level of proof is 41.% Maximum clause weight is 27.% Given clauses 1238.1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption].2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].3 x ^ y = y ^ x. [assumption].4 (x ^ y) ^ z = x ^ (y ^ z). [assumption].5 x ^ (x v y) = x. [assumption].6 x v y = y v x. [assumption].7 (x v y) v z = x v (y v z). [assumption].8 x v (x ^ y) = x. [assumption].9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption].10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)].11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption].12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)].13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption].14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])].15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption].16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)].17 x' ^ x = x ^ R00. [assumption].18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])].19 x'' = x. [assumption].20 x ^ absPCompl(x) = R10. [assumption].21 x v absPCompl(x) = R01. [assumption].22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)].23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption].24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption].25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]....% -------- Comments from original proof -------- % Proof 1 at 27.09 (+ 0.28) seconds. % Length of proof is 240. % Level of proof is 41. % Maximum clause weight is 27. % Given clauses 1238. 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal]. 3 x ^ y = y ^ x. [assumption]. 4 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 5 x ^ (x v y) = x. [assumption]. 6 x v y = y v x. [assumption]. 7 (x v y) v z = x v (y v z). [assumption]. 8 x v (x ^ y) = x. [assumption]. 9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption]. 10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)]. 11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption]. 12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)]. 13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption]. 14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])]. 15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)]. 17 x' ^ x = x ^ R00. [assumption]. 18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])]. 19 x'' = x. [assumption]. 20 x ^ absPCompl(x) = R10. [assumption]. 21 x v absPCompl(x) = R01. [assumption]. 22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)]. 23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption]. 24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption]. 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. ...% -------- Comments from original proof -------- % Proof 1 at 27.09 (+ 0.28) seconds. % Length of proof is 240. % Level of proof is 41. % Maximum clause weight is 27. % Given clauses 1238. 1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y # label(non_clause). [assumption]. 2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal]. 3 x ^ y = y ^ x. [assumption]. 4 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 5 x ^ (x v y) = x. [assumption]. 6 x v y = y v x. [assumption]. 7 (x v y) v z = x v (y v z). [assumption]. 8 x v (x ^ y) = x. [assumption]. 9 x ^ (y v z) = (x ^ (z v (R00 ^ y))) v (x ^ (y v (R00 ^ z))). [assumption]. 10 (x ^ (y v (R00 ^ z))) v (x ^ (z v (R00 ^ y))) = x ^ (z v y). [copy(9),flip(a)]. 11 (x ^ y) v (x ^ z) = x ^ (((x v z) ^ y) v ((x v y) ^ z)). [assumption]. 12 x ^ (((x v y) ^ z) v ((x v z) ^ y)) = (x ^ z) v (x ^ y). [copy(11),flip(a)]. 13 (R00 ^ (x ^ (y v z))) v (y ^ z) = ((R00 ^ (x ^ y)) v z) ^ ((R00 ^ (x ^ z)) v y). [assumption]. 14 (x ^ y) v (R00 ^ (z ^ (x v y))) = ((R00 ^ (z ^ x)) v y) ^ ((R00 ^ (z ^ y)) v x). [copy(13),rewrite([6(6)])]. 15 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 16 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(15),flip(a)]. 17 x' ^ x = x ^ R00. [assumption]. 18 x ^ x' = x ^ R00. [copy(17),rewrite([3(2)])]. 19 x'' = x. [assumption]. 20 x ^ absPCompl(x) = R10. [assumption]. 21 x v absPCompl(x) = R01. [assumption]. 22 x ^ y != R10 | x v y != R01 | absPCompl(x) ^ y = y. [clausify(1)]. 23 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [assumption]. 24 absPCompl(x v y) = absPCompl(x) ^ absPCompl(y). [assumption]. 25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption]. ...
It appears that your assertions for pseudo-complement are too strong.
For instance, are you sure you need both
x ^ absPCompl(x) = R10.
x v absPCompl(x) = R01.
It does no harm to have both. (One of the wiki pages seems to be saying one follows from the other, but that's including other axioms which perhaps carry more restriction.)
Edit: yes I'm sure I need both. If you have this one only: x v absPCompl(x) = R01., that's satisfied by x, absPCompl(x) being any two relations with disjoint headings (perhaps a single attribute each) both non-empty. You need the other axiom to make sure the absPCompl( ) is opposite emptiness, and that it has all the attributes not in x, so their ^ has the heading of R10.
? Wikipedia page that you have referred to has only one of them.
The page on pseudocomplement has only this : x ∧ x* = 0. , which is the one you want to reject, but it does give extra requirements. It does go on to say the definitions necessarily give a 1 element. There's (at least) three wiki pages: on lattices, on complemented lattices, and on pseudo-complements/p-algebras. Also a page on po-sets. They're not well co-ordinated.
Edit: yes, both
x ^ absPCompl(x) = R10.
x being empty makes x* non-empty, and vice versa. So one of the operands to the ^ is empty. So the result is empty. So this holds for Relational lattices.
<absPCompl>(x v y) = <absPCompl>(x) ^ <absPCompl>(y).
are invalid.
I editted my message to say the third they give is wrong (your 25 above). Your second one there (24 above) I think does hold. I've gone through the scenarios of same-headings, disjoint-headings, partial overlaps; for both, neither, one empty. Do you have a counter-example?
Quote from Vadim on June 27, 2021, 6:27 pmQuote from AntC on June 27, 2021, 11:21 amThis one is totally unreasonable/unacceptable:
2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].That's a lattice-wide distribution law. It with the complement law makes the whole lattice a Boolean algebra. Not a Relational lattice.I'm not sure are you agreeing, or disagreeing here. Yes, I'm saying it is a theorem. Therefore, again, at least one of your assumptions is suspect.
This one I rejected in an Edit to my message:
25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption].It's false in a Relational Lattice, under some scenarios. Furthermore I think it introduces a contradiction against some of the Relational-specific axioms (I see you include the Litak axioms), so I think you end up with a system in which you can prove anything -- that seems what I was getting.The assertion #25 can actually be removed from the list of assumptions in the aforementioned distributivity proof. Which points to the other suspects.
Here interpretation of
absPComplin terms of tuple and attribute complement, that is your assertions #2,3,4 proven and 1,5 refuted (#6 is currently in limbo, but I suspect it is correct):#1: x ^ absPCompl(x) = R10.
% Interpretation of size 6 ^ : | 0 1 2 3 4 5 ---+------------ 0 | 0 0 2 2 2 2 1 | 0 1 2 3 4 5 2 | 2 2 2 2 2 2 3 | 2 3 2 3 4 5 4 | 2 4 2 4 4 2 5 | 2 5 2 5 2 5 v : | 0 1 2 3 4 5 ---+------------ 0 | 0 1 0 1 1 1 1 | 1 1 1 1 1 1 2 | 0 1 2 3 4 5 3 | 1 1 3 3 3 3 4 | 1 1 4 3 4 3 5 | 1 1 5 3 3 5 ' : 0 1 2 3 4 5 ---------------- 1 0 3 2 5 4 R00 : 0 R01 : 1 R10 : 2 R11 : 3 c1 : 4 ` : 0 1 2 3 4 5 ---------------- 2 3 0 1 1 1 absPCompl : 0 1 2 3 4 5 ---------------- 3 2 1 0 1 1#2: x v absPCompl(x) = R01.
% -------- Comments from original proof -------- % Proof 1 at 0.08 (+ 0.01) seconds. % Length of proof is 58. % Level of proof is 11. % Maximum clause weight is 31. % Given clauses 96. 1 x v absPCompl(x) = R01. [goal]. 2 x ^ y = y ^ x. [assumption]. 3 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 4 x ^ (x v y) = x. [assumption]. 5 x v y = y v x. [assumption]. 6 x v (x ^ y) = x. [assumption]. 7 x = (x ^ y') v (x ^ y `). [assumption]. 8 (x ^ y') v (x ^ y `) = x. [copy(7),flip(a)]. 9 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 10 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(9),flip(a)]. 11 (x' ^ (y ^ z)')' = (x' ^ y')' ^ (x' ^ z')'. [assumption]. 12 R00 = ((x' ^ x) ` ^ x) `. [assumption]. 13 R00 = ((x ^ x') ` ^ x) `. [para(2(a,1),12(a,2,1,1,1))]. 14 R00 = (x ^ (x ^ x') `) `. [para(2(a,1),13(a,2,1))]. 15 (x ^ (x ^ x') `) ` = R00. [copy(14),flip(a)]. 16 x' ^ x = x ^ R00. [assumption]. 17 x ^ x' = x ^ R00. [para(2(a,1),16(a,1))]. 18 x' v x = x v R11. [assumption]. 19 x v x' = x v R11. [para(5(a,1),18(a,1))]. 20 x ` ^ x = R11 ^ x. [assumption]. 21 x ^ x ` = R11 ^ x. [para(2(a,1),20(a,1))]. 22 absPCompl(x) = x' `. [assumption]. 23 R10 = R10 ^ x. [assumption]. 24 R10 ^ x = R10. [copy(23),flip(a)]. 25 R01 = R01 v x. [assumption]. ...#3: x ^ z = R10 & x v z = R01 -> absPCompl(x) ^ z = z.
1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y. [goal]. 2 x ^ y = y ^ x. [assumption]. 3 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 4 x ^ (x v y) = x. [assumption]. 5 x v y = y v x. [assumption]. 6 x v (x ^ y) = x. [assumption]. 7 x = (x ^ y') v (x ^ y `). [assumption]. 8 (x ^ y') v (x ^ y `) = x. [copy(7),flip(a)]. 9 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 10 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(9),flip(a)]. 11 (x' ^ (y ^ z)')' = (x' ^ y')' ^ (x' ^ z')'. [assumption]. 12 R00 = ((x' ^ x) ` ^ x) `. [assumption]. 13 R00 = ((x ^ x') ` ^ x) `. [para(2(a,1),12(a,2,1,1,1))]. 14 R00 = (x ^ (x ^ x') `) `. [para(2(a,1),13(a,2,1))]. 15 (x ^ (x ^ x') `) ` = R00. [copy(14),flip(a)]. 16 x' ^ x = x ^ R00. [assumption]. 17 x ^ x' = x ^ R00. [para(2(a,1),16(a,1))]. 18 x' v x = x v R11. [assumption]. 19 x v x' = x v R11. [para(5(a,1),18(a,1))]. 20 x ` ^ x = R11 ^ x. [assumption]. 21 x ^ x ` = R11 ^ x. [para(2(a,1),20(a,1))]. 22 absPCompl(x) = x' `. [assumption]. 23 R10 = R10 ^ x. [assumption]. 24 R10 ^ x = R10. [copy(23),flip(a)]. 25 R01 = R01 v x. [assumption]. ...#4: absPCompl(absPCompl(absPCompl(x))) = absPCompl(x).
% -------- Comments from original proof -------- % Proof 1 at 12.53 (+ 0.31) seconds. % Length of proof is 226. % Level of proof is 28. % Maximum clause weight is 31. % Given clauses 1271. 1 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [goal]. 2 x ^ y = y ^ x. [assumption]. 3 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 4 x ^ (x v y) = x. [assumption]. 5 x v y = y v x. [assumption]. 6 (x v y) v z = x v (y v z). [assumption]. 7 x v (x ^ y) = x. [assumption]. 8 x = (x ^ y') v (x ^ y `). [assumption]. 9 (x ^ y') v (x ^ y `) = x. [copy(8),flip(a)]. 10 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 11 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(10),flip(a)]. 12 (x' ^ (y ^ z)')' = (x' ^ y')' ^ (x' ^ z')'. [assumption]. 13 (x ` ^ y') v (x' ^ y `) = (x' v y') ^ (x ` v y `). [assumption]. 14 R00 = ((x' ^ x) ` ^ x) `. [assumption]. 15 R00 = ((x ^ x') ` ^ x) `. [para(2(a,1),14(a,2,1,1,1))]. 16 R00 = (x ^ (x ^ x') `) `. [para(2(a,1),15(a,2,1))]. 17 (x ^ (x ^ x') `) ` = R00. [copy(16),flip(a)]. 18 x' ^ x = x ^ R00. [assumption]. 19 x ^ x' = x ^ R00. [para(2(a,1),18(a,1))]. 20 x' v x = x v R11. [assumption]. 21 x v x' = x v R11. [para(5(a,1),20(a,1))]. 22 R11 = (x' v x `) `. [assumption]. 23 (x' v x `) ` = R11. [copy(22),flip(a)]. 24 x ` ^ x = R11 ^ x. [assumption]. 25 x ^ x ` = R11 ^ x. [para(2(a,1),24(a,1))]. 26 x ` v x = R00 v x. [assumption]. 27 x v x ` = R00 v x. [para(5(a,1),26(a,1))]. 28 absPCompl(x) = x' `. [assumption]. ...#5: absPCompl(x v y) = absPCompl(x) ^ absPCompl(y).
% Interpretation of size 6 ^ : | 0 1 2 3 4 5 ---+------------ 0 | 0 0 2 2 2 2 1 | 0 1 2 3 4 5 2 | 2 2 2 2 2 2 3 | 2 3 2 3 4 5 4 | 2 4 2 4 4 2 5 | 2 5 2 5 2 5 v : | 0 1 2 3 4 5 ---+------------ 0 | 0 1 0 1 1 1 1 | 1 1 1 1 1 1 2 | 0 1 2 3 4 5 3 | 1 1 3 3 3 3 4 | 1 1 4 3 4 3 5 | 1 1 5 3 3 5 ' : 0 1 2 3 4 5 ---------------- 1 0 3 2 5 4 R00 : 0 R01 : 1 R10 : 2 R11 : 3 c1 : 0 c2 : 4 ` : 0 1 2 3 4 5 ---------------- 2 3 0 1 1 1 absPCompl : 0 1 2 3 4 5 ---------------- 3 2 1 0 1 1#6: absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)).
This assertion is verified in QBQL (together with 2,3,4, of course, before running Prover9), this is why I'm quite certain it is correct.
Prover9 is currently over 6hrs into the work, and the model checker progressed till size 29. As you are in Southern Hemisphere in the middle of the winter and might need a house heater, this is the program to run.
I editted my message to say the third they give is wrong (your 25 above). Your second one there (24 above) I think does hold. I've gone through the scenarios of same-headings, disjoint-headings, partial overlaps; for both, neither, one empty. Do you have a counter-example?
Can you please repost your set of axioms? Again, the full set of your axioms 1-6 strengthens RL to Boolean Algebra.
Quote from AntC on June 27, 2021, 11:21 amThis one is totally unreasonable/unacceptable:
2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].That's a lattice-wide distribution law. It with the complement law makes the whole lattice a Boolean algebra. Not a Relational lattice.
I'm not sure are you agreeing, or disagreeing here. Yes, I'm saying it is a theorem. Therefore, again, at least one of your assumptions is suspect.
This one I rejected in an Edit to my message:
25 absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)). [assumption].It's false in a Relational Lattice, under some scenarios. Furthermore I think it introduces a contradiction against some of the Relational-specific axioms (I see you include the Litak axioms), so I think you end up with a system in which you can prove anything -- that seems what I was getting.
The assertion #25 can actually be removed from the list of assumptions in the aforementioned distributivity proof. Which points to the other suspects.
Here interpretation of absPComplin terms of tuple and attribute complement, that is your assertions #2,3,4 proven and 1,5 refuted (#6 is currently in limbo, but I suspect it is correct):
#1: x ^ absPCompl(x) = R10.
% Interpretation of size 6
^ :
| 0 1 2 3 4 5
---+------------
0 | 0 0 2 2 2 2
1 | 0 1 2 3 4 5
2 | 2 2 2 2 2 2
3 | 2 3 2 3 4 5
4 | 2 4 2 4 4 2
5 | 2 5 2 5 2 5
v :
| 0 1 2 3 4 5
---+------------
0 | 0 1 0 1 1 1
1 | 1 1 1 1 1 1
2 | 0 1 2 3 4 5
3 | 1 1 3 3 3 3
4 | 1 1 4 3 4 3
5 | 1 1 5 3 3 5
' :
0 1 2 3 4 5
----------------
1 0 3 2 5 4
R00 : 0
R01 : 1
R10 : 2
R11 : 3
c1 : 4
` :
0 1 2 3 4 5
----------------
2 3 0 1 1 1
absPCompl :
0 1 2 3 4 5
----------------
3 2 1 0 1 1
#2: x v absPCompl(x) = R01.
% -------- Comments from original proof -------- % Proof 1 at 0.08 (+ 0.01) seconds. % Length of proof is 58. % Level of proof is 11. % Maximum clause weight is 31. % Given clauses 96. 1 x v absPCompl(x) = R01. [goal]. 2 x ^ y = y ^ x. [assumption]. 3 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 4 x ^ (x v y) = x. [assumption]. 5 x v y = y v x. [assumption]. 6 x v (x ^ y) = x. [assumption]. 7 x = (x ^ y') v (x ^ y `). [assumption]. 8 (x ^ y') v (x ^ y `) = x. [copy(7),flip(a)]. 9 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 10 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(9),flip(a)]. 11 (x' ^ (y ^ z)')' = (x' ^ y')' ^ (x' ^ z')'. [assumption]. 12 R00 = ((x' ^ x) ` ^ x) `. [assumption]. 13 R00 = ((x ^ x') ` ^ x) `. [para(2(a,1),12(a,2,1,1,1))]. 14 R00 = (x ^ (x ^ x') `) `. [para(2(a,1),13(a,2,1))]. 15 (x ^ (x ^ x') `) ` = R00. [copy(14),flip(a)]. 16 x' ^ x = x ^ R00. [assumption]. 17 x ^ x' = x ^ R00. [para(2(a,1),16(a,1))]. 18 x' v x = x v R11. [assumption]. 19 x v x' = x v R11. [para(5(a,1),18(a,1))]. 20 x ` ^ x = R11 ^ x. [assumption]. 21 x ^ x ` = R11 ^ x. [para(2(a,1),20(a,1))]. 22 absPCompl(x) = x' `. [assumption]. 23 R10 = R10 ^ x. [assumption]. 24 R10 ^ x = R10. [copy(23),flip(a)]. 25 R01 = R01 v x. [assumption]. ...
#3: x ^ z = R10 & x v z = R01 -> absPCompl(x) ^ z = z.
1 x ^ y = R10 & x v y = R01 -> absPCompl(x) ^ y = y. [goal]. 2 x ^ y = y ^ x. [assumption]. 3 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 4 x ^ (x v y) = x. [assumption]. 5 x v y = y v x. [assumption]. 6 x v (x ^ y) = x. [assumption]. 7 x = (x ^ y') v (x ^ y `). [assumption]. 8 (x ^ y') v (x ^ y `) = x. [copy(7),flip(a)]. 9 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 10 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(9),flip(a)]. 11 (x' ^ (y ^ z)')' = (x' ^ y')' ^ (x' ^ z')'. [assumption]. 12 R00 = ((x' ^ x) ` ^ x) `. [assumption]. 13 R00 = ((x ^ x') ` ^ x) `. [para(2(a,1),12(a,2,1,1,1))]. 14 R00 = (x ^ (x ^ x') `) `. [para(2(a,1),13(a,2,1))]. 15 (x ^ (x ^ x') `) ` = R00. [copy(14),flip(a)]. 16 x' ^ x = x ^ R00. [assumption]. 17 x ^ x' = x ^ R00. [para(2(a,1),16(a,1))]. 18 x' v x = x v R11. [assumption]. 19 x v x' = x v R11. [para(5(a,1),18(a,1))]. 20 x ` ^ x = R11 ^ x. [assumption]. 21 x ^ x ` = R11 ^ x. [para(2(a,1),20(a,1))]. 22 absPCompl(x) = x' `. [assumption]. 23 R10 = R10 ^ x. [assumption]. 24 R10 ^ x = R10. [copy(23),flip(a)]. 25 R01 = R01 v x. [assumption]. ...
#4: absPCompl(absPCompl(absPCompl(x))) = absPCompl(x).
% -------- Comments from original proof -------- % Proof 1 at 12.53 (+ 0.31) seconds. % Length of proof is 226. % Level of proof is 28. % Maximum clause weight is 31. % Given clauses 1271. 1 absPCompl(absPCompl(absPCompl(x))) = absPCompl(x). [goal]. 2 x ^ y = y ^ x. [assumption]. 3 (x ^ y) ^ z = x ^ (y ^ z). [assumption]. 4 x ^ (x v y) = x. [assumption]. 5 x v y = y v x. [assumption]. 6 (x v y) v z = x v (y v z). [assumption]. 7 x v (x ^ y) = x. [assumption]. 8 x = (x ^ y') v (x ^ y `). [assumption]. 9 (x ^ y') v (x ^ y `) = x. [copy(8),flip(a)]. 10 x ^ (y' ^ z')' = ((x ^ y)' ^ (x ^ z)')'. [assumption]. 11 ((x ^ y)' ^ (x ^ z)')' = x ^ (y' ^ z')'. [copy(10),flip(a)]. 12 (x' ^ (y ^ z)')' = (x' ^ y')' ^ (x' ^ z')'. [assumption]. 13 (x ` ^ y') v (x' ^ y `) = (x' v y') ^ (x ` v y `). [assumption]. 14 R00 = ((x' ^ x) ` ^ x) `. [assumption]. 15 R00 = ((x ^ x') ` ^ x) `. [para(2(a,1),14(a,2,1,1,1))]. 16 R00 = (x ^ (x ^ x') `) `. [para(2(a,1),15(a,2,1))]. 17 (x ^ (x ^ x') `) ` = R00. [copy(16),flip(a)]. 18 x' ^ x = x ^ R00. [assumption]. 19 x ^ x' = x ^ R00. [para(2(a,1),18(a,1))]. 20 x' v x = x v R11. [assumption]. 21 x v x' = x v R11. [para(5(a,1),20(a,1))]. 22 R11 = (x' v x `) `. [assumption]. 23 (x' v x `) ` = R11. [copy(22),flip(a)]. 24 x ` ^ x = R11 ^ x. [assumption]. 25 x ^ x ` = R11 ^ x. [para(2(a,1),24(a,1))]. 26 x ` v x = R00 v x. [assumption]. 27 x v x ` = R00 v x. [para(5(a,1),26(a,1))]. 28 absPCompl(x) = x' `. [assumption]. ...
#5: absPCompl(x v y) = absPCompl(x) ^ absPCompl(y).
% Interpretation of size 6
^ :
| 0 1 2 3 4 5
---+------------
0 | 0 0 2 2 2 2
1 | 0 1 2 3 4 5
2 | 2 2 2 2 2 2
3 | 2 3 2 3 4 5
4 | 2 4 2 4 4 2
5 | 2 5 2 5 2 5
v :
| 0 1 2 3 4 5
---+------------
0 | 0 1 0 1 1 1
1 | 1 1 1 1 1 1
2 | 0 1 2 3 4 5
3 | 1 1 3 3 3 3
4 | 1 1 4 3 4 3
5 | 1 1 5 3 3 5
' :
0 1 2 3 4 5
----------------
1 0 3 2 5 4
R00 : 0
R01 : 1
R10 : 2
R11 : 3
c1 : 0
c2 : 4
` :
0 1 2 3 4 5
----------------
2 3 0 1 1 1
absPCompl :
0 1 2 3 4 5
----------------
3 2 1 0 1 1
#6: absPCompl(absPCompl(x ^ y)) = absPCompl(absPCompl(x)) ^ absPCompl(absPCompl(y)).
This assertion is verified in QBQL (together with 2,3,4, of course, before running Prover9), this is why I'm quite certain it is correct.
Prover9 is currently over 6hrs into the work, and the model checker progressed till size 29. As you are in Southern Hemisphere in the middle of the winter and might need a house heater, this is the program to run.
I editted my message to say the third they give is wrong (your 25 above). Your second one there (24 above) I think does hold. I've gone through the scenarios of same-headings, disjoint-headings, partial overlaps; for both, neither, one empty. Do you have a counter-example?
Can you please repost your set of axioms? Again, the full set of your axioms 1-6 strengthens RL to Boolean Algebra.
Quote from AntC on June 30, 2021, 7:58 amQuote from Vadim on June 27, 2021, 6:27 pmQuote from AntC on June 27, 2021, 11:21 amThis one is totally unreasonable/unacceptable:
2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].That's a lattice-wide distribution law. It with the complement law makes the whole lattice a Boolean algebra. Not a Relational lattice.I'm not sure are you agreeing, or disagreeing here. Yes, I'm saying it is a theorem. Therefore, again, at least one of your assumptions is suspect.
I now have a set of axioms in which that distributivity is not a theorem; but in which I have a proof of the uniqueness of
DUMakaR00. I'll publish in a later message; I'm not yet sure which are the minimal set. There's plenty of ugly axioms, including the clunkyR1halfto force 'lop-sidedness' into the structure.
Here interpretation of
absPComplin terms of tuple and attribute complement, ...Then equally we can express your tuple and attribute complements in terms of
absPCompl, probably needing also to axiomatise that relations with the same heading form a sublattice that's a Boolean algebra. That's now included in my axioms.Since the sublattice of empty relations from
DUMdown to lattice bottom form a Boolean algebra; and the sublattice of full-as-possible relations fromDEEdown toR11form another Boolean algebra; and those two sublattices are in 1:1 correspondence, I've axiomatised this journey:
- start with any relation
x, drop down to emptifyx NatJoin DUM;- go 'across the floor' to the empty relation with complement heading:
hCompl ^ (x NatJoin DUM) = R10. hCompl v (x NatJoin DUM) = DUM.;- climb up to the full-as-possible relation with that heading
hCompl v R11;- go 'across the ceiling' to the full-as-possible relation with complement-of-complement heading:
mCompl ^ (hCompl v R11) = R11. mCompl v (hCompl v R11) = DEE.- You must be at
x v R11.- Note
R11 =df absPCompl(R00).And is unique providingR00akaDUMis unique.
Prover9 is currently over 6hrs into the work, and the model checker progressed till size 29. As you are in Southern Hemisphere in the middle of the winter and might need a house heater, this is the program to run.
Heh heh yes. Over 30 mins to prove
R00/DUMis unique.Yesterday we got a polar blast: hailstones in the city, snow on the hills, mountain passes closed, flights cancelled, inter-island ferries confined to harbour. I'm afraid running proofs wasn't enough to keep the house warm, I need a Bitcoin mining operation.
Can you please repost your set of axioms? Again, the full set of your axioms 1-6 strengthens RL to Boolean Algebra.
Time for a recap:
- Within a Relational lattice, there are lots of Boolean algebras embedded/sublattices.
- But the overall structure is not a Boolean algebra: distributivity doesn't hold; complements are not unique.
- Every element has a pseduo-complement that's unique, and many of the p-algebra laws hold (but not all).
- The characteristic structure is that there are N5 sublattices embedded all over the place; no M3 sublattices; no benzene /six-sided sublattices.
- So complementation is lop-sided: if
x's complements are non-unique, then all ofx's complements are uniquely complemented and double-complement comes back tox.- More to the point, if
x's complements are non-unique,xmust be empty IOWx NatJoin DUM = x.- (The reverse is not true:
xmight be non-empty but still have a unique complement -- as for example withDEE.)- We can say that if
x's complements are non-unique, the candidate complementsz1, z2, ...all have the same headingz1 NatJoin DUM = z2 NatJoin DUM = ...- I want to explore more that each convex sublattice of a relational lattice is uniquely pseudocomplemented; and exhibits the same 'lop-sided' structure -- that is, if you didn't pick a sublattice that's a Boolean algebra. In particular,
R00/DUMstill discriminates the unique vs non-unique complements.Now I didn't see any of this lop-sidedness getting picked up in the Litak et al paper. That is, if they talk about it, it's in such obscure language it's gone over my head. And I'm pretty sure it's not captured in their axioms. From discussions with them, they didn't want to investigate deeper, because it makes their axioms ugly.
Addit: The Litak paper has an example of a N5 lattice (Figure 2/top of page 7); but amongst their counter-examples is an M3, that also includes a benzenz six-sided sublattice ('Clause 2'/top of page 11). I claim that figure can't be a Relational lattice, there's missing 'nodes' that would stop it being M3, also stop it being benzene; although certainly filling in the missings would give plenty of embedded N5's. Litak et al are mis-characterising.
Quote from Vadim on June 27, 2021, 6:27 pmQuote from AntC on June 27, 2021, 11:21 amThis one is totally unreasonable/unacceptable:
2 x ^ (y v z) = (x ^ y) v (x ^ z) # label(non_clause) # label(goal). [goal].That's a lattice-wide distribution law. It with the complement law makes the whole lattice a Boolean algebra. Not a Relational lattice.I'm not sure are you agreeing, or disagreeing here. Yes, I'm saying it is a theorem. Therefore, again, at least one of your assumptions is suspect.
I now have a set of axioms in which that distributivity is not a theorem; but in which I have a proof of the uniqueness of DUM aka R00. I'll publish in a later message; I'm not yet sure which are the minimal set. There's plenty of ugly axioms, including the clunky R1half to force 'lop-sidedness' into the structure.
Here interpretation of
absPComplin terms of tuple and attribute complement, ...
Then equally we can express your tuple and attribute complements in terms of absPCompl, probably needing also to axiomatise that relations with the same heading form a sublattice that's a Boolean algebra. That's now included in my axioms.
Since the sublattice of empty relations from DUM down to lattice bottom form a Boolean algebra; and the sublattice of full-as-possible relations from DEE down to R11 form another Boolean algebra; and those two sublattices are in 1:1 correspondence, I've axiomatised this journey:
- start with any relation
x, drop down to emptifyx NatJoin DUM; - go 'across the floor' to the empty relation with complement heading:
hCompl ^ (x NatJoin DUM) = R10. hCompl v (x NatJoin DUM) = DUM.; - climb up to the full-as-possible relation with that heading
hCompl v R11; - go 'across the ceiling' to the full-as-possible relation with complement-of-complement heading:
mCompl ^ (hCompl v R11) = R11. mCompl v (hCompl v R11) = DEE. - You must be at
x v R11. - Note
R11 =df absPCompl(R00).And is unique providingR00akaDUMis unique.
Prover9 is currently over 6hrs into the work, and the model checker progressed till size 29. As you are in Southern Hemisphere in the middle of the winter and might need a house heater, this is the program to run.
Heh heh yes. Over 30 mins to prove R00/DUM is unique.
Yesterday we got a polar blast: hailstones in the city, snow on the hills, mountain passes closed, flights cancelled, inter-island ferries confined to harbour. I'm afraid running proofs wasn't enough to keep the house warm, I need a Bitcoin mining operation.
Can you please repost your set of axioms? Again, the full set of your axioms 1-6 strengthens RL to Boolean Algebra.
Time for a recap:
- Within a Relational lattice, there are lots of Boolean algebras embedded/sublattices.
- But the overall structure is not a Boolean algebra: distributivity doesn't hold; complements are not unique.
- Every element has a pseduo-complement that's unique, and many of the p-algebra laws hold (but not all).
- The characteristic structure is that there are N5 sublattices embedded all over the place; no M3 sublattices; no benzene /six-sided sublattices.
- So complementation is lop-sided: if
x's complements are non-unique, then all ofx's complements are uniquely complemented and double-complement comes back tox. - More to the point, if
x's complements are non-unique,xmust be empty IOWx NatJoin DUM = x. - (The reverse is not true:
xmight be non-empty but still have a unique complement -- as for example withDEE.) - We can say that if
x's complements are non-unique, the candidate complementsz1, z2, ...all have the same headingz1 NatJoin DUM = z2 NatJoin DUM = ... - I want to explore more that each convex sublattice of a relational lattice is uniquely pseudocomplemented; and exhibits the same 'lop-sided' structure -- that is, if you didn't pick a sublattice that's a Boolean algebra. In particular,
R00/DUMstill discriminates the unique vs non-unique complements.
Now I didn't see any of this lop-sidedness getting picked up in the Litak et al paper. That is, if they talk about it, it's in such obscure language it's gone over my head. And I'm pretty sure it's not captured in their axioms. From discussions with them, they didn't want to investigate deeper, because it makes their axioms ugly.
Addit: The Litak paper has an example of a N5 lattice (Figure 2/top of page 7); but amongst their counter-examples is an M3, that also includes a benzenz six-sided sublattice ('Clause 2'/top of page 11). I claim that figure can't be a Relational lattice, there's missing 'nodes' that would stop it being M3, also stop it being benzene; although certainly filling in the missings would give plenty of embedded N5's. Litak et al are mis-characterising.
Quote from AntC on June 30, 2021, 10:28 amWhy/how does the lop-sidedness arise?
The characteristic structure is that there are N5 sublattices embedded all over the place; no M3 sublattices; no benzene /six-sided sublattices.
Suppose there's only relations with heading
{ B Bool }(other thanDEE, DUM). Then we get
DEEREL {} { TUP{} }≡1
DUM REL {} { }≡a
REL {B Bool} { TUP{B True}, TUP{B False}}≡cakaR11
REL {B Bool} { TUP{B True} }≡b1
REL {B Bool} { TUP{B False} }≡b2
REL {B Bool} { }≡0akaR10/Dumpty
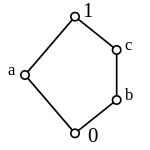
Note there are two N5 lattices here (two candidates corresponding to node labelled
b) -- both have the two-leg side throughDUM; one has the three-leg side throughREL{ TUP{B True} }; the other three-legs throughREL{ TUP{B False} }.Suppose there's relations with headings
{C Char}, {C Char, B Bool}amot. Then relation values include
REL {C Char} { TUP{C 'C'}, TUP{C 'B'} }≡1
DUM REL {C Char} { TUP{C 'C'} }≡a
REL {C Char, B Bool} { TUP{C 'C', B True}, TUP{C 'C', B False},≡
TUP{C 'B', B True}, TUP{C 'B', B False} }c
REL {C Char, B Bool} { TUP{C 'C', B True}, TUP{C 'C', B False},≡
TUP{C 'B', B True} }b1
REL {C Char, B Bool} { TUP{C 'C', B True}, TUP{C 'C', B False},≡
TUP{C 'B', B False} }b2
REL {C Char, B Bool} { TUP{C 'C', B True}, TUP{C 'C', B False} }≡0
≡ 1here means top within the sublattice≡ 0here means bottom within the sublatticeAgain there are two N5 lattices here (two candidates corresponding to node labelled
b) -- both have the two-leg side throughREL{ TUP{C 'C'} }; the two three-leg sides each go through a 3-tuple lattice.Each step is the minimum possible distance -- either by removing one tuple (
1-a,c-bn-0); or by widening by a single attribute (1-c,a-0) -- then we must form the Cartesian product for all possible values of the added attribute's type.Everywhere there's an embedded N5 sublattice, it's because the three-legged side has a wider heading than the two-legged side. The two top/left (
1,a) have the same narrower heading; the three right/bottom (c,bn,0) have the same wider heading.For relations with differing headings, there's only one way you might not get an N5: that's when the 'added' attribute's type has only one possible value. I'd call this degenerate, but let's work an example. Say attribute
Ahas typeOnly_Awith only one valueTHE_A:
DEEREL {} { TUP{} }≡1
DUM REL {} { }≡a
REL {A Only_A} { TUP{A THE_A} }≡cakaR11(no relation) ≡
b
REL {A Only_A} { }≡0
But providing there's at least one attribute in the schema whose type has cardinality > 1, we still get N5:
DEEREL {A Only_A} { TUP{A THE_A} }≡1
DUM REL {A Only_A} { }≡a
REL {A Only_A, B Bool} { TUP{A THE_A, B True},≡
TUP{A THE_A, B False}}cakaR11
REL {A Only_A, B Bool} { TUP{A THE_A, B True} }≡b1
REL {A Only_A, B Bool} { TUP{A THE_A, B False} }≡b2
REL {A Only_A, B Bool} { }≡0
There's no benzene/six-sided sublattice (which would have an extra node on lhs between
a,0), because on the lhs we are removing one tuple only.There's no M3 diamond sublattice, because there's not three distinct ways to descend from (sub)lattice top: either you remove a tuple; or you add an attribute; there's no middle way. (To both remove a tuple and add an attribute must be two distinct steps.)
I should emphasise again a point from the earlier thread: a Relational lattice is not just a random collection of lattice values: it must include all possible relation values that can be formed by projecting subset-headings and taking all possible combinations of tuples for each possible heading. A corollary is that when considering any sublattice, take the convex sublattice -- that is all elements on any path from sublattice top to sublattice bottom.
By convention, I draw these structures following the above diagrams, such that headings get wider left-to-right, and values get emptier top-to-bottom.
Within not only the overall lattice structure, but also within any minimal N5 or larger convex sublattice:
- The (sub)lattice complement of
ais ambiguous between {c,bn} -- that is those values with heading same as (sub)lattice bottom.- For the (sub)lattice 'pseudocomplement' by definition resolve to the 'highest' of those -- that is,
c.- The (sub)lattice complement of
c, anybnis uniquelya-- that is, the only value with heading same as (sub)lattice top.- The (sub)lattice complement of top
1is uniquely bottom0and vice versa.
Why/how does the lop-sidedness arise?
-
The characteristic structure is that there are N5 sublattices embedded all over the place; no M3 sublattices; no benzene /six-sided sublattices.
Suppose there's only relations with heading { B Bool } (other than DEE, DUM). Then we get
DEE REL {} { TUP{} } ≡ 1
|
 |
|
Note there are two N5 lattices here (two candidates corresponding to node labelled b) -- both have the two-leg side through DUM; one has the three-leg side through REL{ TUP{B True} }; the other three-legs through REL{ TUP{B False} }.
Suppose there's relations with headings {C Char}, {C Char, B Bool} amot. Then relation values include
REL {C Char} { TUP{C 'C'}, TUP{C 'B'} } ≡ 1
|
 |
|
≡ 1 here means top within the sublattice |
≡ 0 here means bottom within the sublattice |
Again there are two N5 lattices here (two candidates corresponding to node labelled b) -- both have the two-leg side through REL{ TUP{C 'C'} }; the two three-leg sides each go through a 3-tuple lattice.
Each step is the minimum possible distance -- either by removing one tuple (1 - a, c - bn - 0); or by widening by a single attribute (1 - c, a - 0) -- then we must form the Cartesian product for all possible values of the added attribute's type.
Everywhere there's an embedded N5 sublattice, it's because the three-legged side has a wider heading than the two-legged side. The two top/left (1, a) have the same narrower heading; the three right/bottom (c, bn, 0) have the same wider heading.
For relations with differing headings, there's only one way you might not get an N5: that's when the 'added' attribute's type has only one possible value. I'd call this degenerate, but let's work an example. Say attribute A has type Only_A with only one value THE_A:
DEE REL {} { TUP{} } ≡ 1
|
 |
(no relation) ≡
|
But providing there's at least one attribute in the schema whose type has cardinality > 1, we still get N5:
DEE REL {A Only_A} { TUP{A THE_A} } ≡ 1
|
 |
|
There's no benzene/six-sided sublattice (which would have an extra node on lhs between a, 0), because on the lhs we are removing one tuple only.
There's no M3 diamond sublattice, because there's not three distinct ways to descend from (sub)lattice top: either you remove a tuple; or you add an attribute; there's no middle way. (To both remove a tuple and add an attribute must be two distinct steps.)
I should emphasise again a point from the earlier thread: a Relational lattice is not just a random collection of lattice values: it must include all possible relation values that can be formed by projecting subset-headings and taking all possible combinations of tuples for each possible heading. A corollary is that when considering any sublattice, take the convex sublattice -- that is all elements on any path from sublattice top to sublattice bottom.
By convention, I draw these structures following the above diagrams, such that headings get wider left-to-right, and values get emptier top-to-bottom.
Within not only the overall lattice structure, but also within any minimal N5 or larger convex sublattice:
- The (sub)lattice complement of
ais ambiguous between {c,bn} -- that is those values with heading same as (sub)lattice bottom. - For the (sub)lattice 'pseudocomplement' by definition resolve to the 'highest' of those -- that is,
c. - The (sub)lattice complement of
c, anybnis uniquelya-- that is, the only value with heading same as (sub)lattice top. - The (sub)lattice complement of top
1is uniquely bottom0and vice versa.